L’analyse en Composantes Principales (ACP) est une méthode d’analyse des données utilisée pour l’étude exploratoire ou la réduction d’un grand tableau n × p de données quantitatives, où n désigne le nombre d’individus et p le nombre de variables quantitatives. L’analyse des données consiste essentiellement à établir quelles sont les relations existant entre les observations, entre les variables, et entre les
observations et les variables.
Objectifs
Etudier les interrelations entre un assez grand nombre de variables
Regrouper ces variables dans des groupes limités appelés
facteurs ou composantes.
Etablir entre ces groupes de variables une hiérarchie basée
essentiellement sur la valeur explicative de chacun d’eux
Chap 1 Analyse en composantes principales
Exemple
On se propose d’étudier une marque de voiture, on relève les
variables suivantes: prix, vitesse, look, sécurité, confort. lesquelles
sont les plus importantes ?
Par sondage à un échantillon de clients ;
Les variables seront notées de 1 à 10,
où 1 = Pas du tout important et 10 = Très important.
Supposons que l’analyse a donné les résultats suivants:

Chap 1 Analyse en composantes principales
Exemple
Il permet de dégager l’attitude des cliens vis-à-vis de ces variables,
Une importance considérable est allouée au facteur 1 dans le quel la
sécurité est plus importante que le confort (voiture allemande vs
voiture française),
Pour le facteur 2 le prix précède l’importance de la vitesse.
L’analyse en composantes principales, dans cet exemple, a bien
rempli son rôle :
réduire les données et donner une certaine explication aux
choix effectués par les répondants.
Intuitivement, on cherchera le sous-espace donnant la meilleure visualisation possible de notre nuage de points. Un bon choix consiste à rechercher la plus grande dispersion (le plus grand étalement) possible des projections dans le sous-espace choisi. On est amené ainsi à chercher une rotation de notre système d’axes initial (les variables) permettant de mieux voir notre nuage.
Recherche des variables similaires. celles-ci doivent faire partie
d’un même ensemble : mesure de la satisfaction, de l’intérêt, etc. ;
matrice des corrélations entre les variables choisies ;
Dégagerles facteurs
Rotation des axes, qui désigne les facteurs les plus
importants selon leur degré d’inertie (de variance
expliquée) ;
Lecture des tests les plus importants;
Interprétation des résultats au plan des décisions et de l’action
Voici un tableau de scores attribuées à 9 individus dans 5 matières
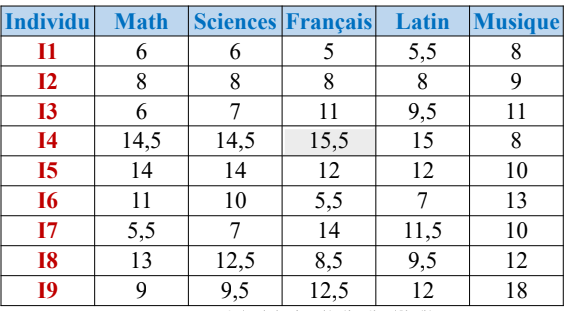
Pratique de l’ACP
On calculer les moyennes arithmétiques et les écarts-types des 5
variables quantitatives qui seront résumées dans le tableau suivant :
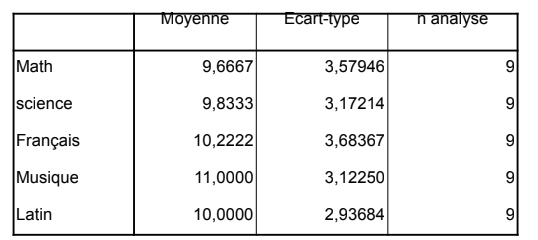
Ces données doivent êtes centrées et réduites pour éliminer l’effet
taille des données et avoir des valeurs sans unité. Cette opération
consiste à centrer les données puis les diviser par l’ ́écart type:
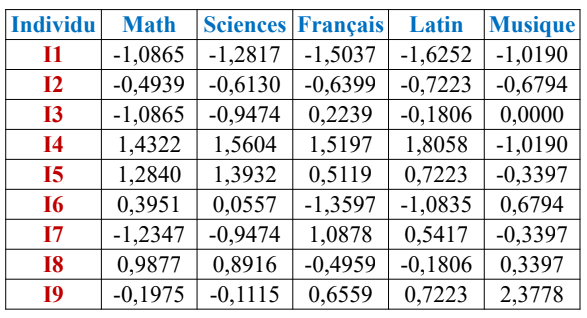

2. Pratique de l’ACP
La démarche de l’ACP est la suivante : En partant de 5 axes factoriels qui correspondent aux 5 variables, elle va les réduire tout en maximisant la quantité d’informations dans le nuage de points (ou) bien réduire la perte d’informations).
Ainsi l’objectif est de déterminer un plan factoriel formé par des axes sur lesquels on effectuera une projection des variables. Evidemment le nuage initial est complexe puisque le nombre des dimensions est élevé (égal au nombre de variables 5).
Pratique de l’ACP
Les 5 axes factoriels qui correspondent aux 5 variables:
2. Pratique de l’ACP
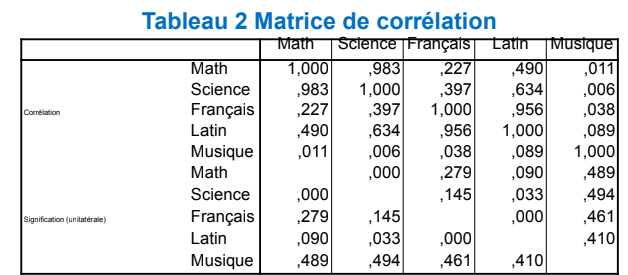
2.1 Matrice de corrélation
La corrélation entre les deux variables Math et Science est de 0,983 cela prouve une forte corrélation positive. Par contre entre Math et Musique elle est de 0,011 soit une absence de corrélation. Remarquons qu’il n’existe pas de corrélation négative dans notre exemple.
A ne pas oublier que la corrélation n’entraine pas nécessairement l’existence d’une relation, alors que la réciproque est toujours vraie.
2. Pratique de l’ACP
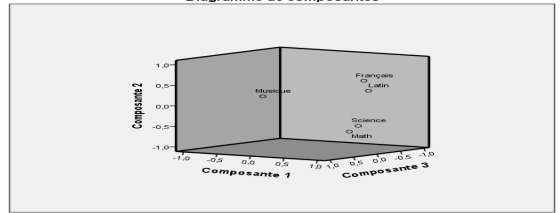
2.2 Nuage de points
Le nuage de points peut être lu de deux manières : soit à partir des individus soit à partir des variables.
2. Pratique de l’ACP
2.2 Nuage de points
Nuage des individus
Notre exemple porte sur 9 individus, alors le nuage des individus sera le nuage produit par les les 9 points, pris dans un espace de dimension 5 (le nombre de variables). On définit l’inertie totale (c’est la quantité d’informations contenue dans le nuage) comme étant la somme des distances euclidiennes du point O (puisqu’il s’agit d’une ACP normée) aux différents points du nuage.
Pratique de l’ACP
2.2 Nuage de points
Nuage des individus
En appliquant le théorème de Pythagore et la distance métrique sur
IRn, l’inertie totale du nuage est
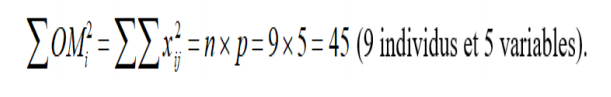
Pratique de l’ACP
2.2 Nuage de points
Nuage des individus
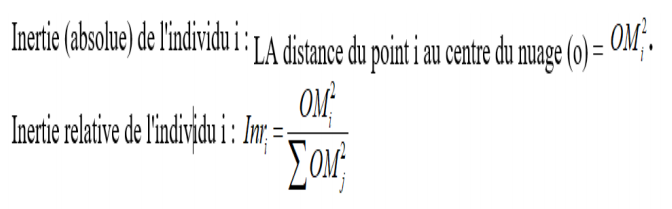
Chap 1 Analyse en composantes principales
2. Pratique de l’ACP
2.2 Nuage de points
Nuage des variables
De la même manière on peut définir la nuage des variables. Ainsi
l’inertie absolue de chaque variable est n, son inertie relative est 1/p…
L’objectif de l’ACP est de réduire les variables d’une part par
l’obtention de nouvelles composantes factorielles obtenues comme
combinaison linéaire des variables initiales. Ainsi il sera formé les
composantes CP1, CP2,… selon l’ordre décroissant de signification.
Autre dit la première composante va représenter le nuage initial avec
la plus grande proportion, la 2ème composante sera la deuxième,
etc..
Egalement il faudrait ajouter que ces composantes sont indépendantes (géométriquement orthogonales) donc leur covariance est nulle .
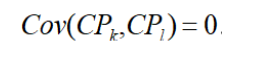
la variance d’une composante principale CPk est égale à la k-ième valeur propre.
A ce niveau d’analyse on emprunte les connaissances de l’algèbre
linéaire. En fait diagonaliser une matrice revient à trouver des vecteurs propres dégagés eux même des valeurs propres de cette même matrice. Les valeurs propres représentent la même information (l’inertie du nuage de points) dans deux systèmes d’axes orthonormés différents.
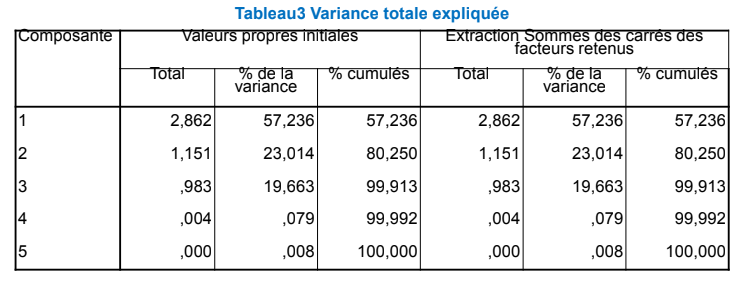
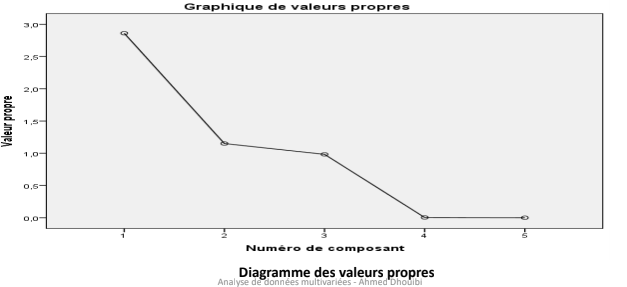
Il existe plusieurs méthodes : règle de Kaiser, règle du coude etc.
D’où l’idée de ne garder que les valeurs propres (et directions propres) qui représentent au moins 20% de variation.
Variante : on observe une brusque décroissance des valeurs propres entre la 3è et la 4è valeur propre.
Au final, on décide de ne garder que 2 valeurs propres.
2. Pratique de l’ACP
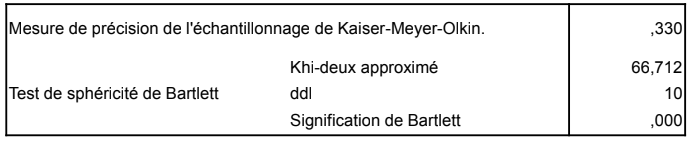
2.4 Indice KMO et test de Bartlett
Ce sont deux indicateurs pour évaluer la qualité d’une ACP. Plus
l’indice KMO est proche de 0.8 plus l’ACP est bonne et plus il s’éloigne
de 0.8 elle devient non significative.
Le test de sphéricité de Bartlett propose une mesure globale en
s’appuyant sur une démarche statistique. Il vise à détecter dans
quelle mesure la matrice de corrélation R=(rij)(p x p) calculée sur nos
données (matrice observée) diverge significativement de la matrice
unité (matrice théorique sous hypothèse nulle H0).
2. Pratique de l’ACP
2.4 Indice KMO et test de Bartlett
Essayer de procéder à un résumé est illusoire lorsque l’hypothèse
nulle n’est pas démentie par les données.
En revanche, il est possible de compresser l’information, jusqu’à quel
point on ne le sait pas, en un nombre plus réduit de facteurs lorsque
l’hypothèse nulle est rejetée.
Cela ne veut pas dire pour autant que nous allons trouver des
informations intéressantes dans notre ACP
2. Pratique de l’ACP
2.4 Indice KMO et test de Bartlett
Pour mesurer le lien entre les variables, nous calculons le
déterminant |R| de la matrice de corrélation.
Sous H0, |R| = 1 ;
s’il y a des colinéarités parfaites, nous aurions |R| = 0.
Ici également, fixer des valeurs seuils est difficile.
Chap 1 Analyse en composantes principales
2. Pratique de l’ACP
2.4 Indice KMO et test de Bartlett
Lorsque |R| est inférieur à 0.00001, il y a de très fortes redondances
dans les données c.-à-d. elles ne recèlent qu’un seul type
d’information. Le résultat sera d’une très grande trivialité (ex. les
personnes de grande taille sont plus lourdes, courent plus vite,
sautent plus haut et ont des grands pieds). A l’inverse, lorsque |R| se
rapproche de 1, l’ACP ne servira pas à grand-chose car les variables
sont quasiment orthogonales deux à deux. Le test de Bartlett vise
justement à vérifier si l’on s’écarte significativement de cette situation
de référence |R| = 1.
Indice KMO et test de Bartlett
2. Pratique de l’ACP
2.4 Indice KMO et test de Bartlett
Lorsque |R| est inférieur à 0.00001, il y a de très fortes redondances
dans les données c.-à-d. elles ne recèlent qu’un seul type
d’information. Le résultat sera d’une très grande trivialité (ex. les
personnes de grande taille sont plus lourdes, courent plus vite,
sautent plus haut et ont des grands pieds). A l’inverse, lorsque |R| se
rapproche de 1, l’ACP ne servira pas à grand-chose car les variables
sont quasiment orthogonales deux à deux. Le test de Bartlett vise
justement à vérifier si l’on s’écarte significativement de cette situation
de référence |R| = 1.
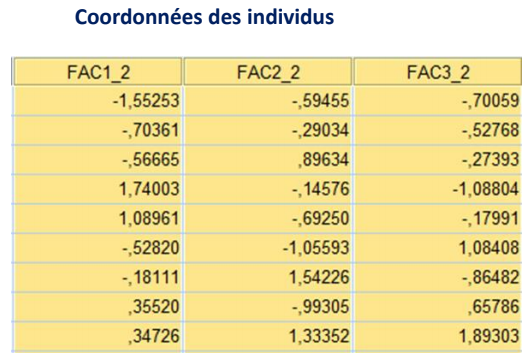
2.5 Résultats relatifs aux individus
Coefficients des individus
Les scores des individus sont les valeurs des composantes factorielles
sur les individus.
Pratique de l’ACP
2.5 Résultats relatifs aux individus
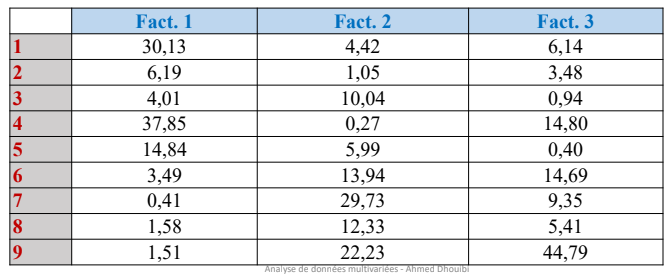
Contributions des individus
La contribution relative d’un individu i à la formation de la
composante principale k est définie par :

Pratique de l’ACP
2.5 Résultats relatifs aux individus
Contributions des individus seront les suivantes :
Pratique de l’ACP
2.5 Résultats relatifs aux individus
Qualités de la représentation des individus
La qualité de la représentation d’un individu i par la composante
principale k est définie par :
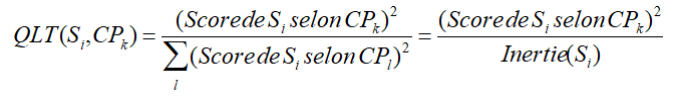
Pratique de l’ACP
2.5 Résultats relatifs aux individus
Par exemple :
Géométriquement, la qualité de la représentation d’un individu i
par la composante principale.

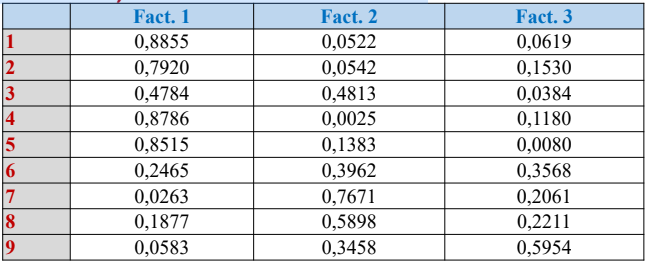
Résultats relatifs aux individus
Cosinus carrés, basées sur les corrélations
2. Pratique de l’ACP
2.5 Résultats relatifs aux individus
Les qualités de représentation sont additives. Par exemple, la qualité
de représentation d’un individu i par le plan (CP1, CP2) est donnée par

Résultats relatifs aux individus
Pour l’individu 1 1, la qualité de représentation par le plan
factoriel 1×2 est : 0,8855+0,0522=0,9377.
Cette valeur représente le carré du cosinus de l’angle que fait avec
le plan (CP1, CP2).
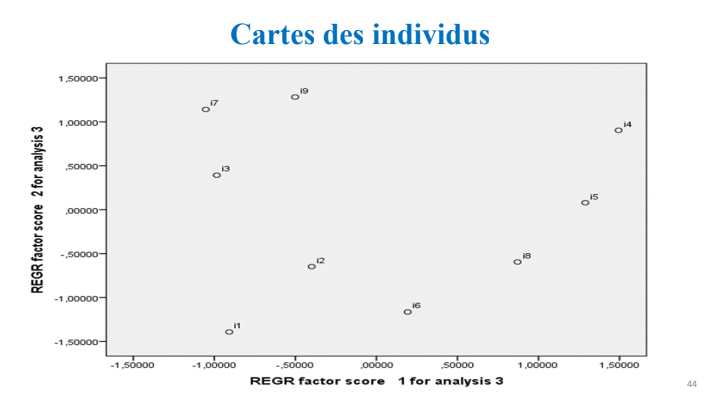
2.5 Résultats relatifs aux variables
Coordonnées des variables
De même, les variables ont des coordonnées factorielles sur les deux
axes.
On observe une grande corrélation entre l’axe 1 et les variables Math
et Science, cela prouve que l’axe 1 est formé par les matières
scientifiques.
L’axe 2 est dominé par les variables Français et Latin cela peut indiquer
que cet axe est formé par les matières littéraires.
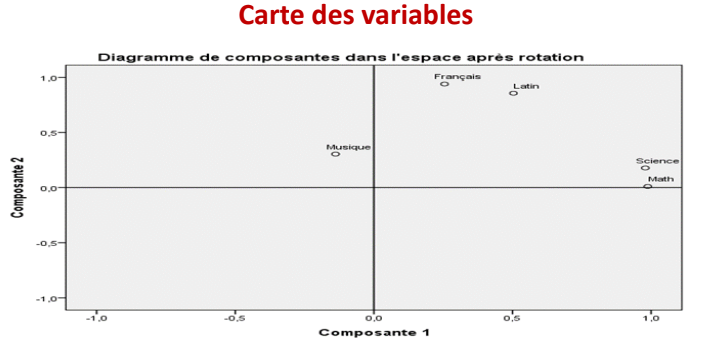
Coordonnées des variables
De même, les variables ont des coordonnées factorielles sur les deux
axes.
On observe une grande corrélation entre l’axe 1 et les variables Math
et Science, cela prouve que l’axe 1 est formé par les matières
scientifiques.
L’axe 2 est dominé par les variables Français et Latin cela peut indiquer
que cet axe est formé par les matières littéraires.
2.5 Résultats relatifs aux variables
Les coordonnées sont données par le tableau suivant :
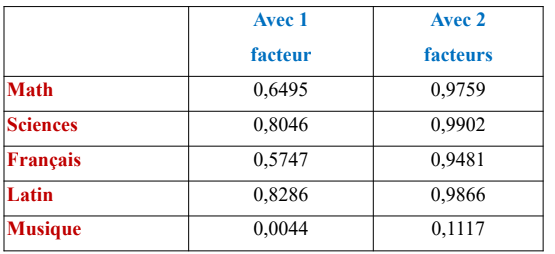
2.6 Autres résultats:
Le tableau des coefficients des variables peut être lu de deux façons :
– il permet de calculer les valeurs des composantes principales à partir
des variables centrées réduites de départ
– il permet de retrouver les valeurs des variables centrées réduites de
départ à partir des valeurs des composantes principales.
Vecteurs propres de la matrice de corrélation Variables actives seules
2.6 Autres résultats:
Vecteurs propres de la matrice de corrélation Variables actives seules
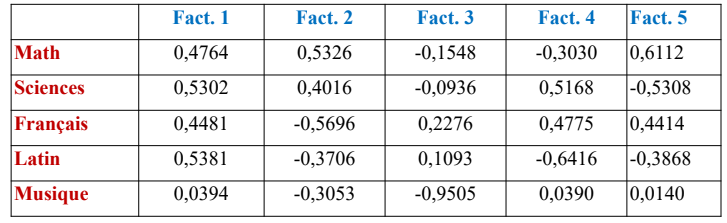
2.6 Autres résultats:
On observera que :
– chaque ligne représente un vecteur de norme 1
– chaque colonne représente un vecteur de norme 1
– deux « vecteurs ligne » quelconques sont orthogonaux
– deux « vecteurs colonne » quelconques sont orthogonaux
Pour l’individu 1, les variables de départ ont pour valeurs
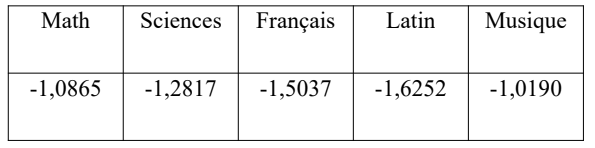
Pratique de l’ACP
2.6 Autres résultats:
On retrouve ainsi le score de cet individu sur la première composante
principale :
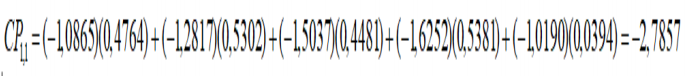
2.6 Autres résultats:
Pour l’individu 1, les scores sur les 5 composantes principales sont :
Fact. 1 Fact. 2 Fact. 3 Fact. 4 Fact. 5
-2,7857 0,6764 0,7368 -0,0482 -0,0332
2.6 Autres résultats:
Les valeurs propres pourraient également être calculées à partir du
tableau, comme variances des composantes principales. Autrement
dit, on pourrait à l’aide du tableau des coefficients, retrouver tous les
résultats indiqués ci-dessus.
Ce tableau permet également de retrouver les saturations des
variables, en multipliant les coefficients correspondant à chaque
facteur par la racine carrée de la valeur propre correspondante.
2.7 Rotation des axes:
Une méthode orthogonale « repose sur la
maximalisation de la somme des variances des
carrés des saturations dans chaque colonne ;
il s’ensuit une augmentation de certaines saturations et la
diminution des autres.
La formule est : MPF * MSC = MR où : MPF = matrice des
premiers facteurs ; MSC = matrice de transformation sinus, cosinus ;
MR = matrice avec rotation.
Pratique de l’ACP
2.7 Rotation des axes (varimax):
Grâce à cette méthode de rotation d’axes, chacune des variables de
l’ensemble aura le poids le plus élevé possible sur un facteur et le
poids le plus faible possible sur les autres facteurs. Il s’agit donc de
maximaliser les corrélations faibles de façon à opérer une
discrimination entre les facteurs et de parvenir à une explication plus
intéressante des relations entre les variables.